Quiz 10 2 inscribed angles answers – Welcome to Quiz 10.2: Inscribed Angles Answers, a comprehensive guide to understanding the properties, formulas, and applications of inscribed angles. This quiz, designed for academic exploration, delves into the intriguing world of geometry, where circles and angles intertwine.
As we embark on this journey, we will uncover the secrets of inscribed angles, exploring their relationship to circles, examining their unique properties, and unlocking their practical applications in various fields. Get ready to expand your knowledge and master the art of inscribed angles!
1. Definition and Overview of Inscribed Angles
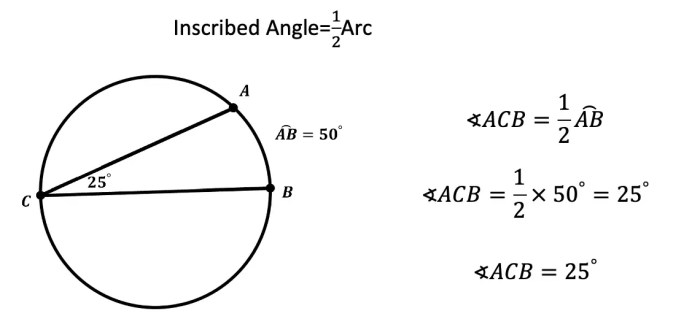
An inscribed angle is an angle whose vertex lies on a circle and whose sides intersect the circle. Inscribed angles are related to the intercepted arc, which is the part of the circle cut off by the angle’s sides. The measure of an inscribed angle is half the measure of its intercepted arc.
Inscribed angles have several important properties. For example, the opposite angles of an inscribed quadrilateral add up to 180 degrees. Additionally, the inscribed angle theorem states that the measure of an inscribed angle is equal to half the difference of the measures of the intercepted arcs.
Inscribed angles are used in a variety of applications, including geometry, trigonometry, and architecture. For example, inscribed angles can be used to find the measure of an arc or to construct regular polygons.
2. Formula and Theorem for Inscribed Angles
The formula for finding the measure of an inscribed angle is:
m∠ABC = (1/2)mAB
where m∠ABC is the measure of the inscribed angle, mAB is the measure of the intercepted arc, and ∠ABC is the inscribed angle.
The inscribed angle theorem states that the measure of an inscribed angle is equal to half the difference of the measures of the intercepted arcs. In other words:
m∠ABC = (1/2)(mAC
mBC)
where m∠ABC is the measure of the inscribed angle, mAC and mBC are the measures of the intercepted arcs, and ∠ABC is the inscribed angle.
The inscribed angle theorem can be used to solve a variety of problems involving inscribed angles. For example, it can be used to find the measure of an arc or to construct regular polygons.
3. Properties and Applications of Inscribed Angles

Inscribed angles have several important properties. For example:
- The opposite angles of an inscribed quadrilateral add up to 180 degrees.
- The measure of an inscribed angle is equal to half the difference of the measures of the intercepted arcs.
- The measure of an inscribed angle is always less than 180 degrees.
Inscribed angles are used in a variety of applications, including:
- Geometry: Inscribed angles can be used to find the measure of an arc or to construct regular polygons.
- Trigonometry: Inscribed angles can be used to solve trigonometric equations.
- Architecture: Inscribed angles can be used to design buildings and other structures.
Questions and Answers: Quiz 10 2 Inscribed Angles Answers
What is the formula for finding the measure of an inscribed angle?
The formula for finding the measure of an inscribed angle is: m∠ = 1/2(m⌒)
How do you prove the inscribed angle theorem?
The inscribed angle theorem can be proven using the properties of chords and the fact that the sum of the angles in a triangle is 180 degrees.
What are some real-world applications of inscribed angles?
Inscribed angles are used in architecture, design, and navigation. For example, they are used to design arches, domes, and other curved structures.